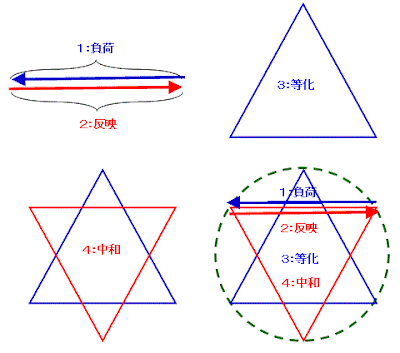
さて、ここで問題ですが、「等化」をどのように考えればよいかということです。そもそも「対化」する二項というのは、まさしく「対立項」でもあり、互いが互いにとって特殊な存在であるとも言えます。つまり、敵対関係にあるがごとく、全く違う立場にある存在であり、互いが互いを同等な存在として見ないとも言えます。こうした「対化」の関係にある二項が「たいして違わない、単なるバリエーションの違いでしかない」といった観点に立てることが「等化」ではないかと思うます。
少し抽象的すぎますので、例を挙げておきますと、「青」と「赤」というと寒色と暖色という感じで全く違う感じであり、「対化」的な存在だと言えますが、どちらも「色」という意味では「等化」されていると言ってもいいのではないでしょうか。「形」や「数」ではないが「色」の一種として「等化」できるというわけです。ではそれに対して「中和」はどんな感じかと言えば、「青」と「赤」を混ぜた色としての「紫」という「色」は「中和」と呼べるのではないかと考えます。ただし、「等化」と「中和」は互いに反転関係であると言われると、この色の喩えではピンと来なくなってしまいます。
あえて言うなら、「青」と「赤」で次の関係としてピンと来る色は、「緑」だと言えば、「光の三原色」の残りの一色であり、「黄」だと言えば、「色の三原色」の残りの一色です。この「光の三原色」と「色の三原色」をそれぞれ「見るための色」と「見られるための色」と名付ければ、「緑」と「黄」が「対化」の様相を呈してきます。
次に、前述の「対化」の幾何学的描像の延長線上に「等化」の幾何学的描像を考えてみましょう。前述のように、+1と-1の「対化」の関係が「原点Oを中心とする180度の回転」で表せるなら、ちょうどその真ん中の「原点Oを中心とする90度の回転」(反時計回りを正とする90度の回転)というものはどういうことになるか考えてみます。
等化の描像(1)
通常、+1から-1に至る過程の半分という意味では、「+i」が対応すると考えます。ここで登場する「i」とは、「虚数単位」です。
どういうことかと言うと、私たちが普通に使っている数というのは、「実在する数」という意味で「実数」と呼ばれます。この実数は2回掛け合わせる(2乗する)と必ず正の数になります。つまり、xが実数であるなら、
というわけです。実際、
となって、正の数も負の数も2乗すると、正の数になります
ところが、あえてここで、
となる数xというものを考えます。すると、数学の2次方程式を解いたり、物理学の諸現象を説明する上で、とても説明しやすくなるのです。訳のわからない数を導入して説明しやすくなるとは、詭弁のようであるが、構造的には綺麗な説明ができるようになります。そこで、
となる数 のうち、正の方を「虚数単位」と呼んで「i」と書く。つまり、あえて書くなら、
のうち、正の方を「虚数単位」と呼んで「i」と書く。つまり、あえて書くなら、
と定義するというわけです。これが「虚数」と呼ばれるのは、実際にはそのままではあり得ないような「虚」なる数だからです。あり得ない数が自然界にはあるのだから、これほどパラドクシカルな詭弁はないような気がします。その基準となる単位を、「虚数単位」と呼ぶわけです。これに対して、1は実数の基準となる単位であるから、「実数単位」と呼ばれます。
この実数単位を基準とする「実数軸」という数直線と、虚数単位を基準とする「虚数軸」という数直線を直交させてできる平面が、「複素数平面」(あるいは「ガウス平面」)と呼ばれる平面です。
すると、前述の「原点Oを中心とする90度の回転」というものは「実数軸を複素数平面上で回転する操作」ということになります。これは結果的に、「ある数に虚数単位iを掛ける操作」のことです。まとめると、
・ある数に-1を掛ける操作…複素数平面上での「原点Oを中心とする180度の回転」
・ある数に+iを掛ける操作…複素数平面上での「原点Oを中心とする90度の回転」
ということになる。
等化の描像(2)
果たして、この「原点Oを中心とする90度の回転」は「等化」と言っていいのでしょうか。疑問に感じるところです。実際、原点Oを中心とする反時計回りに90度の回転を4回続けると、一周して元の場所に戻ってきます。途中経過を見てみると、最初の90度の回転で、+1は+iになり、次の90度の回転で、+iは-1になり、続く90度の回転で、-1は-iになり、最後の90度の回転で、-iは+1になるということです。こうして、「原点Oを中心とする回転」の中で+1と-1を見た場合、それは既に対立項ではなく、単なる回転操作の一つのバリエーションでしかなくなっていることに気付くはずです。これこそが、「等化の本質」なのだと思います。